摘要:生活中,圆周率π、自然常数e和黄金分割率Φ的应用场景广泛。π在几何、工程、建筑等领域中用于计算圆的周长和面积;e在金融、物理等科目中体现复利增长和自然现象的模型化;Φ则应用于艺术、建筑和设计等领域,实现美学与实用性的完美结合。这些常数不仅在数学领域有重要意义,也在日常生活和工作中发挥着重要作用。
本文目录导读:
在我们的日常生活中,许多看似复杂深奥的数学概念,如圆周率π、自然常数e和黄金分割率Φ,实际上在悄无声息地发挥着巨大的作用,这些数学概念不仅在数学领域占据重要地位,而且在建筑、艺术、工程、金融等多个领域也有着广泛的应用,本文将探讨这些数学概念在我们生活中的实际应用场景。
圆周率π的应用场景
1、建筑与工程设计:在建筑工程设计中,圆周率π经常应用于圆形和椭圆形的建筑结构设计,如体育场、圆形广场等。π还用于计算管道、容器的体积和表面积。
2、烹饪:在烹饪中,我们常常遇到与圆相关的食物,如圆形蛋糕、饼干等,这时,圆周率π可以帮助我们计算食材的用量,确保食物的口感和外观。
3、金融与投资:圆周率π在金融领域也有应用,如计算复利、折现等问题,投资者可以利用π值进行精确的投资计算,以获取更高的收益。
自然常数e的应用场景
1、金融市场:自然常数e在金融领域的应用主要体现在金融衍生品定价方面,如期权、期货等,e值在这些金融产品的定价公式中起到关键作用。
2、生物学与医学:在生物学和医学领域,e常用于描述生物种群的增长规律,人口增长模型、细菌繁殖等过程中都会涉及到e的应用。
3、计算机科学:在计算机科学中,e也扮演着重要角色,在数据压缩、加密算法等领域,e值的应用有助于提高算法的性能和安全性。
黄金分割率Φ的应用场景
1、艺术与设计:黄金分割率Φ在艺术与设计领域具有广泛的应用,许多著名的艺术品和建筑设计都遵循了黄金分割原则,如古希腊的帕特农神庙、蒙娜丽莎的微笑等,黄金分割使得艺术作品在视觉上更加和谐、美观。
2、摄影与图像处理:在摄影和图像处理中,黄金分割被广泛应用于构图,通过将图像的重要元素放置在黄金分割点上,可以使照片更具吸引力。
3、金融市场与投资决策:黄金分割在金融市场和投资决策中也有应用,投资者在分析股票价格、市场趋势时,可以借鉴黄金分割的原理,以辅助决策。
4、自然界的黄金分割现象:在自然界中,黄金分割现象也屡见不鲜,植物的分支、某些动物的体型比例等都遵循了黄金分割的原则。
综合应用实例
在日常生活中,许多场景都涉及到了圆周率π、自然常数e和黄金分割率Φ的综合应用,在建筑设计中,设计师可能需要同时考虑到圆形的建筑结构和生物种群增长模型(涉及e)以及视觉上的美观(涉及Φ),在金融投资领域,投资者可能需要利用π进行复利计算,同时结合黄金分割原理分析市场趋势,以做出更明智的投资决策。
生活中的许多场景都与我们看似深奥的数学概念息息相关,如圆周率π、自然常数e和黄金分割率Φ,这些数学概念在建筑工程、金融投资、艺术等领域发挥着重要作用,了解这些数学概念的实际应用,不仅有助于我们更好地理解生活中的现象,还能提高我们的决策能力,随着科技的进步和数学的发展,这些数学概念在日常生活中的应用将越来越广泛。

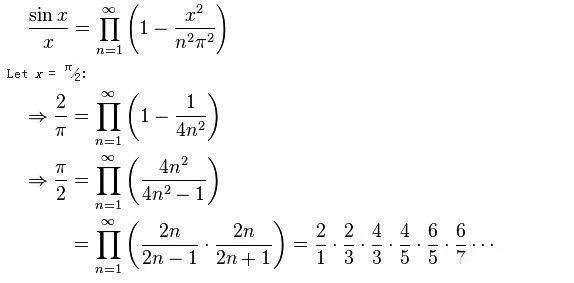
 京ICP备11000001号
京ICP备11000001号