摘要：开普勒通过观测行星运动，发现行星绕太阳运行的轨道呈现椭圆形。他通过对行星位置、速度和时间的精确测量，收集大量数据并运用数学方法进行分析，最终揭示了行星轨道椭圆形的奥秘。这一发现对天文学领域产生了深远影响，为后来的天体物理学和宇宙学研究奠定了基础。

本文目录导读：

1. 开普勒的背景与成就
2. 开普勒如何计算行星轨道为椭圆形

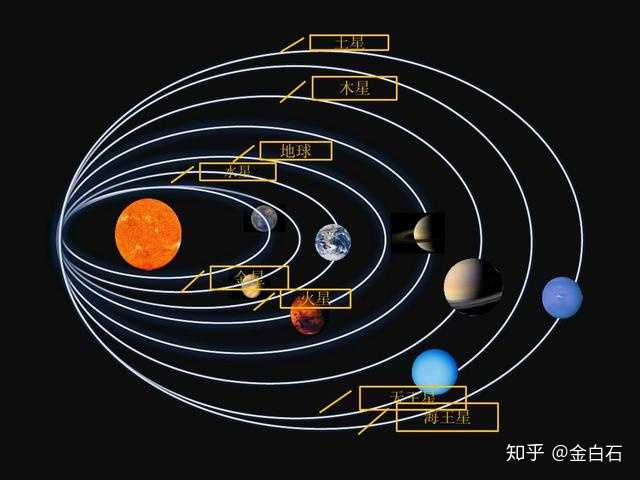
在浩瀚的宇宙中，行星的运动轨迹一直吸引着人们的关注，早在古希腊时期，天文学家们就开始探索行星的运动规律，真正揭开行星轨道椭圆形的奥秘的，是17世纪的德国天文学家约翰内斯·开普勒，他通过对行星运动的大量观测数据进行分析，提出了行星运动三大定律，其中第二定律直接揭示了行星轨道的椭圆形特征，本文将详细介绍开普勒是如何结合观测与数学推导，揭示出行星轨道椭圆形的秘密。

开普勒的背景与成就

约翰内斯·开普勒是17世纪德国著名天文学家，他在哥白尼和伽利略等天文学家的基础上，进一步揭示了天体运动的基本规律，开普勒通过对火星等行星的观测数据进行分析，提出了行星运动的三大定律，第二定律为我们揭示了行星轨道的椭圆形特征，这一时期的天文学发展，为后来的牛顿万有引力定律的建立奠定了基础。

开普勒如何计算行星轨道为椭圆形

开普勒通过对火星等行星的观测数据进行分析，结合数学推导，逐步揭示出行星轨道椭圆形的特征，具体过程如下：

1、收集观测数据

开普勒拥有大量的天文观测数据，这些数据主要来源于他对行星的长期观测，这些数据为他揭示行星运动的规律提供了重要的依据。

2、数据分析与初步发现

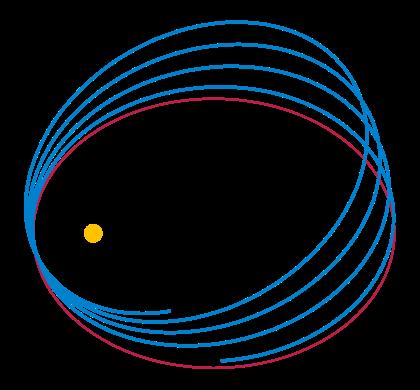
开普勒对观测数据进行了详细的分析，他发现，行星绕太阳运动的轨迹并非简单的圆形，而是呈现出一种特殊的形状，这个形状与我们现在所熟知的椭圆形状非常相似。

3、提出行星运动三大定律

在数据分析的基础上，开普勒提出了行星运动的三大定律，第二定律（也称面积定律）指出，行星与太阳连线在相同时间内扫过的面积相等，这一规律暗示了行星轨道的椭圆形特征，因为在一个椭圆轨道中，行星离太阳最近的点（近日点）速度最快，离太阳最远的点（远日点）速度最慢，这样才能保证连接行星和太阳的线段在相同时间内扫过的面积保持不变。

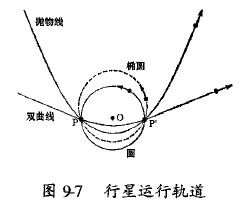
4、椭圆轨道的数学推导

为了验证自己的猜想，开普勒进行了深入的数学推导，他发现，只有椭圆轨道能够同时满足第二定律和第三定律（周期定律），第三定律指出，行星的椭圆轨道半长轴的立方与公转周期的平方成正比，这一规律为开普勒提供了强有力的证据，证明他的猜想是正确的。

通过大量的观测数据和数学推导，开普勒成功揭示出行星轨道的椭圆形特征，这一发现对天文学产生了深远的影响，它为牛顿万有引力定律的建立提供了重要的依据，开普勒的研究方法为我们提供了一种新的科学思维方式，即将观测与数学推导相结合，从而揭示自然界的奥秘，开普勒的研究还激发了后世天文学家们对天体运动规律的进一步探索。

开普勒通过观测、分析和数学推导，成功揭示出行星轨道椭圆形的奥秘，这一成就标志着人类对天体运动规律的认识达到了一个新的高度，我们回顾开普勒的研究历程，不仅是为了纪念他的伟大成就，更是为了从中汲取科学精神和方法论启示，展望未来，我们期待更多的科学家能够继承开普勒的精神，不断探索宇宙的奥秘，为人类的天文学发展做出更大的贡献。