摘要：本文旨在深化理解多重积分、格林公式与曲线积分的概念和应用，超越单纯的计算层面。通过深入探索这些数学工具的本质，旨在揭示它们在解决实际问题中的重要作用，如求解物理问题、分析几何图形等。本文旨在帮助读者从更高层次上掌握这些数学工具，提高解决实际问题的能力。

本文目录导读：

1. 多重积分的理解
2. 格林公式的理解
3. 曲线积分的理解
4. 深入理解的方法

数学中的多重积分、格林公式以及曲线积分是高级微积分概念，它们在物理、工程、经济学和其他领域有着广泛的应用，许多学生在学习这些概念时，往往只满足于套用计算公式进行机械的计算，缺乏对它们的深入理解和应用，本文将探讨如何透彻理解这些概念，而不仅仅是停留在计算层面。

多重积分的理解

多重积分是单一积分的扩展，用于计算高维空间下的体积和面积，为了透彻理解多重积分，我们需要明白其背后的几何意义，我们需要理解积分区域是如何定义的，以及如何通过划分和求和来估计积分值，我们还需要理解多重积分在解决实际问题中的应用，如计算物理现象的体积分或求解概率分布函数等，为了深化理解，我们可以尝试通过解决一些实际问题来应用多重积分，而不仅仅是解决抽象的数学问题。

格林公式的理解

格林公式是一个在平面上将某一点的函数值与其邻域内的函数值相关联的公式，理解格林公式需要我们从其背后的物理意义出发，理解其如何在平面上传递信息，我们还需要理解格林公式在各种应用中的使用，如求解偏微分方程、计算曲面积分等，为了深化理解格林公式，我们可以通过探索其在不同领域的应用，并尝试从不同的角度理解和证明格林公式。

曲线积分的理解

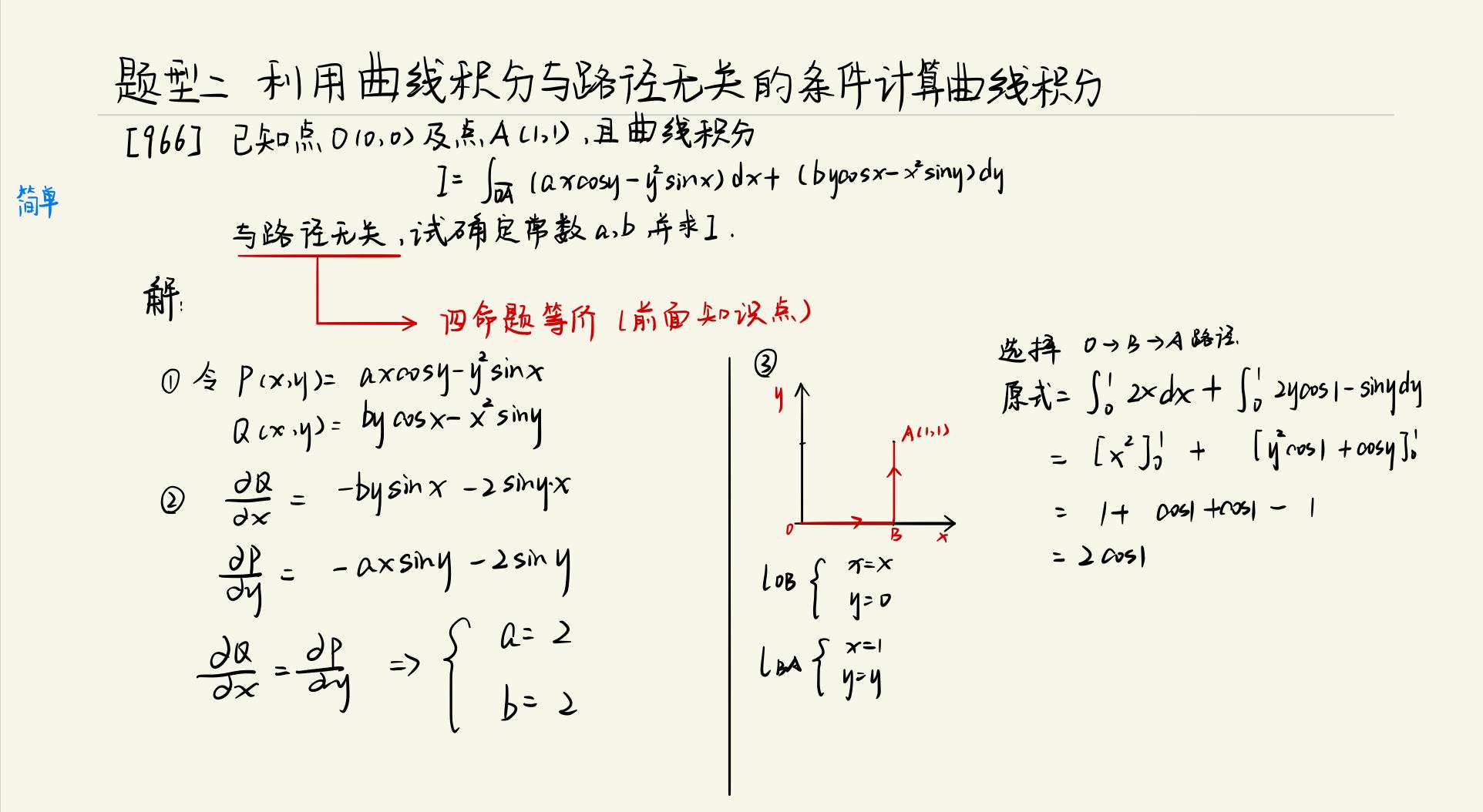
曲线积分是对曲线上的函数值进行积分的一种数学工具，为了透彻理解曲线积分，我们需要明白其背后的几何意义，即如何计算曲线上的面积或长度，我们还需要理解曲线积分在实际问题中的应用，如求解物理现象中的路径积分或计算经济学中的边际效应等，为了深化理解曲线积分，我们可以尝试通过解决一些实际问题来应用曲线积分，并尝试从不同的角度理解和证明曲线积分的性质。

深入理解的方法

为了透彻理解多重积分、格林公式和曲线积分，我们需要采用多种方法，我们需要多做计算实践，通过解决各种实际问题来应用这些概念，我们需要阅读相关的数学物理方程和理论书籍，了解这些概念的历史背景和来源，我们还需要多做案例分析，了解这些概念在实际问题中的应用，我们需要勤于思考，尝试从不同的角度理解和证明这些概念的性质和定理。

数学中的多重积分、格林公式和曲线积分是高级微积分概念，它们在解决实际问题中有着广泛的应用，为了透彻理解这些概念，我们需要明白其背后的几何意义和应用背景，并尝试通过解决实际问题来应用这些概念，我们还需要多做计算实践、阅读相关书籍、做案例分析和勤于思考等方法来深化理解，只有这样，我们才能真正掌握这些概念，并将其应用于实际问题的解决中。

在学习过程中，我们可能会遇到许多困难和挑战，只要我们坚持不懈地努力，不断地探索和实践，就一定能够取得进步，希望本文能够为那些正在学习多重积分、格林公式和曲线积分的读者提供一些启示和帮助。